Particle lifetimes from the uncertainty principle

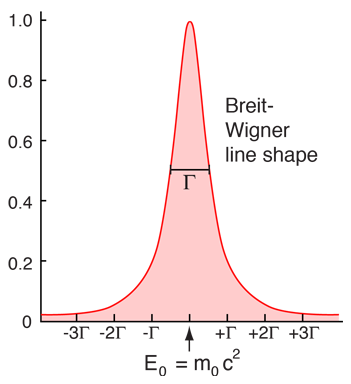The Breit-Wigner distribution is similar to a gaussian near the peak, but the tails of the curve are flatter.

The uncertainty principle provides a tool for characterizing the very short-lived products produced in high energy collisions in accelerators. The uncertainty principle in the form suggests that for particles with extremely short lifetimes, there will be a significant uncertainty in the measured energy. The measurment of the mass energy of an unstable particle a large number of times gives a distribution of energies called a Lorentzian or a Breit-Wigner distribution.

If the width of this distribution at half-maximum is labeled Γ , then the uncertainty in energy &#916E could be reasonably expressed as

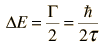
where the particle lifetime τ is taken as the uncertainty in time τ = Δt.

In high energy scattering experiments, the energy uncertainty &#916E can be determined and the lifetime implied from it. In other cases, the lifetime is most conveniently measured and the "particle width" in energy implied from that lifetime measurement.</p> <SCRIPT LANGUAGE ="JavaScript"> function tcal(){fh=document.forms[0];gam=fh.gb.value*Math.pow(10,fh.gp.value);h=4.1356692*Math.pow(10,-15);tt=h/(gam*2*Math.PI);fh.tb.value=snb(tt);fh.tp.value=snp(tt);fh.gmev.value=display(gam/Math.pow(10,6));fh.ggev.value=display(gam/Math.pow(10,9))} function gcal(){fh=document.forms[0];tt=fh.tb.value*Math.pow(10,fh.tp.value);h=4.1356692*Math.pow(10,-15);gam=h/(tt*2*Math.PI);fh.gb.value=snb(gam);fh.gp.value=snp(gam);ee=1.602177*Math.pow(10,-19);fh.gmev.value=display(gam/Math.pow(10,6));fh.ggev.value=display(gam/Math.pow(10,9))} function gu(e){fh=document.forms[0];fh.gmev.value=display(e);fh.ggev.value=display(e/1000);fh.gb.value=snb(e*Math.pow(10,6));fh.gp.value=snp(e*Math.pow(10,6));tcal()} <!-- the following routines handle the conversion to and from scientific notation--> <!-- sn(b,p) converts number with power of 10 to a number--> function sn(b,p){return b*Math.pow(10,p)} <!--snp(x) returns the power of 10 for a number--> function snp(x){return Math.round(Math.log(x)/Math.LN10)} <!--snb(x) returns the base of number with which to multiply the power of 10--> function snb(x){return x/Math.pow(10,snp(x))} <!--svb(b,p) takes input base and power and scales to make base between 1 and 10, returns base--> function svb(b,p){n=sn(b,p);return snb(n)} <!--svp(b,p) takes input base and power and scales to make base between 1 and 10, returns power--> function svp(b,p){n=sn(b,p);return snp(n)} <!--snbv and snpv handle the possibility of a negative number which blows up in the above routine--> function snbv(x){if(x<0)return -snb(-x);else{return snb(x)}} function snpv(x){if(x<0)return snp(-x);else{return snp(x)}} <!--display(x) checks to see if a number is too small or too large to fit in a 6-space field, and if so, displays ellipsis ...--> function display(x){xx=x;if(x<Math.pow(10,-4))xx="...";if(x>.99*Math.pow(10,5))xx="...";return xx} <!--default values are set for parameters which have zero values--> <!--There is value in having an overall default function for a calculation to provide values for all parameter which you dont want to default to zero--> function def(){fh=document.forms[0];if (fh.gb.value==0)fh.gb.value=1;if (fh.tb.value==0)fh.tb.value=1} </script> <FORM method="" action=""> <table><tr><td>For linewidth</td><td><img src="imgqua/gamcap.gif"></td><td> =<INPUT Type="text" Name="gb" Value="" Size="6"onChange=tcal()>x10^<INPUT Type="text" Name="gp" Value="" Size="4"onChange=tcal()> eV = <INPUT Type="text" Name="gmev" Value="" Size="6"onChange=gu(this.value)>MeV = <INPUT Type="text" Name="ggev" Value="" Size="6"onChange=gu(this.value*1000)>GeV,</td></tr></table> and the energy uncertainty can be taken to be half of that value. <table><tr><td>The associated lifetime is</td><td><img src="imgqua/tau.gif"></td><td> = <INPUT Type="text" Name="tb" Value="" Size="6"onChange=gcal()>x10^<INPUT Type="text" Name="tp" Value="" Size="6"onChange=gcal()>seconds.</td></tr></table> </form> <p>&#915 is often referred to as the "natural line width". It is of great importance in high energy accelerator physics where it provides the means for determining the ultrashort lifetimes of particles produced. For optical spectroscopy it is a minor factor because the natural linewidth is typically 10^-7 eV, about a tenth as much as the <a href="../atomic/broaden.html#c1">Doppler broadening</a>. Another source of linewidth is the recoil of the source, but that is negligible in the optical range.</p> <p> For nuclear transitions involving gamma emission in the 0.1-1 MeV range, the recoil width is typically much greater than the natural line width. The recoil of the emitting nucleus implies that the emitted gamma photon cannot be absorbed by an identical nucleus because its energy is reduced by an amount greater than the natural line width of potential absorbing levels. Mossbauer discovered that the absorption could be accomplished by putting the source on a rotating arm to give it enough speed to compensate for the recoil effect. The <a href="../nuclear/mossb.html#c1">Mossbauer effect</a> became a useful experimental tool when it was discovered that the recoil could be suppressed by putting the emitting nucleus in a crystal lattice. The emitted gammas then exhibited something close to the natural linewidth and could be absorbed by other identical nuclei.</p> <center><table BORDER="1" CELLSPACING="2" CELLPADDING= "2"><tr><td><a href="../nuclear/mossfe.html#c1">Natural linewidth in iron</a></td></tr></table></center> <center><table BORDER="1" CELLSPACING="2" CELLPADDING= "2"><tr><td><a href="../time.html#c1">A brief overview of time.</a></td></tr></table></center> </TD> <TD WIDTH="66" align=center><a href="../hframe.html">Index</a><br><br><a href="../unccon.html#c1">Uncertainty principle concepts</a><br><br>Reference<br><a href="../quaref.html#c1">Rohlf</a><br>Ch 5</TD></TR> <TR> <TD HEIGHT="17">&nbsp;<table><tr><td width= "450"><A HREF="../hph.html"> HyperPhysics</A>*****<A HREF="../quacon.html#quacon"> Quantum Physics </A></td><td align=right><font size="-1"><i>R Nave</i></font></td></tr></table></TD> <TD><a href="Javascript:history.go(-1)">Go Back</a></TD></TR> </TABLE> <BR> <BR> <BR> <BR> <BR> <BR> <BR> <BR> <BR> <BR> </BODY> </HTML>