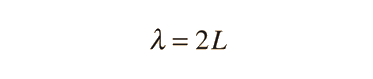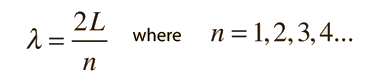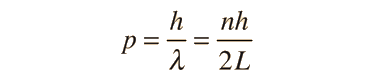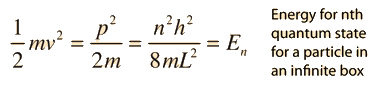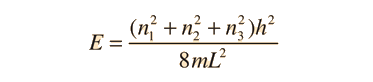Schrodinger Equation

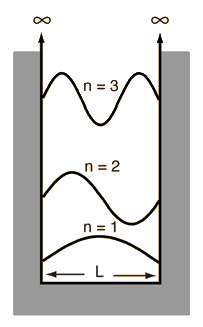
The Schrodinger equation plays the role of Newton's laws and conservation of energy in classical mechanics - i.e., it predicts the future behavior of a dynamic system. It is a wave equation in terms of the wavefunction which predicts analytically and precisely the probability of events or outcome. The detailed outcome is not strictly determined, but given a large number of events, the Schrodinger equation will predict the distribution of results.

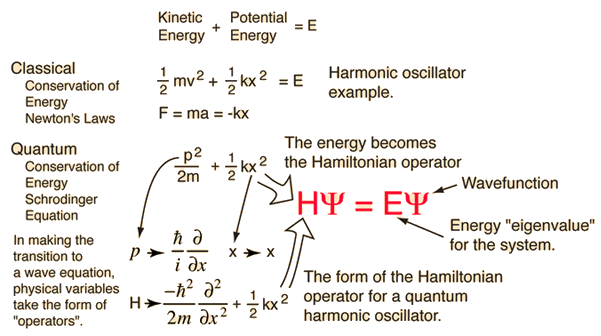
The kinetic and potential energies are transformed into the Hamiltonian which acts upon the wavefunction to generate the evolution of the wavefunction in time and space. The Schrodinger equation gives the quantized energies of the system and gives the form of the wavefunction so that other properties may be calculated.

Particle in a Box

The idealized situation of a particle in a box with infinitely high walls is an application of the Schrodinger equation which yields some insights into particle confinement. The wavefunction must be zero at the walls and the solution for the wavefunction yields just sine waves. The longest wavelength is and the higher modes have wavelengths given by When this is substituted into the DeBroglie relationship it yields momentum

Particle in a Box

Calculation

When the momentum expression for the particle in a box is used to calculate the energy associated with the particle Though oversimplified, this indicates some important things about bound states for particles: 1. The energies are quantized and can be characterized by a quantum number n 2. The energy cannot be exactly zero. 3. The smaller the confinement, the larger the energy required. If a particle is confined into a rectangular volume, the same kind of process can be applied to a three-dimensional "particle in a box", and the same kind of energy contribution is made from each dimension. The energies for a three-dimensional box are This gives a more physically realistic expression for the available energies for contained particles. This expression is used in determining the density of possible energy states for electrons in solids.

Particle in a Box Calculation

For a one-dimensional particle in a box , the particle energy for a box of dimension L can be calculated below. For a three-dimensional box there will be three values for the quantum number n. The energies for each dimension could be calculated and added. The implication of that addition is that it takes more energy to confine a particle in three dimensions than in one, and that the minimum confinement energy for a 3D box of dimension L is three times that of a 1D box.

L = x 10^ m = a₀ = fermi* = proton radii**,

and mass = x 10^ kg = m_e = m_p = MeV/c²,

then the energy for state n = for a one-dimensional box is

E = x 10^joules = eV = MeV = GeV.

The ground state of a three-dimensional box of dimension L can be obtained by setting n=1 for all three dimensions, giving an energy three times the ground state energy of the one-dimensional box. The ground state for the three-dimensional box would be E3D ground = x 10^joules = eV = MeV = GeV. * 1 fermi = 10-15m. ** Classical radius of proton calculated using the nominal nuclear density of 2.3x1017kg/m3